Parce que vous n'avez jamais été très bon en maths, ou parce que vous êtes bon mais que vous n'arrivez pas à expliquer des théorèmes pas trop compliqués à vos enfants ou que vous êtes allergique à la craie, voici qui devrait vous aider. Plutôt que de tout expliquer avec des schémas pas toujours clairs, Internet et les ingénieux internautes ont décidé de mettre tout ça en gif et ça fonctionne. Quoi de mieux qu'un gif animé pour visualiser dans l'espace Thalès, Pythagore et ce qu'est un cosinus ? Interro en fin de top, soyez attentifs et sortez votre rapporteur.
- Théorème de Pythagore
Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit. Avec de l'eau, tout devient clair.
Source photo : mathgifs - Le triangle rectangle
Un triangle inscrit dans un cercle et dont un côté est un diamètre est un triangle rectangle. Autrement dit, le diamètre d'un cercle forme un triangle rectangle avec n'importe quel point de ce cercle.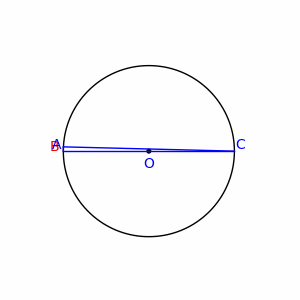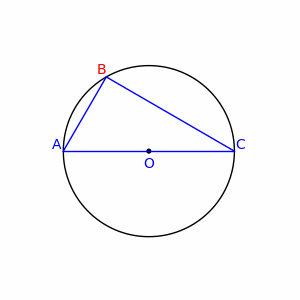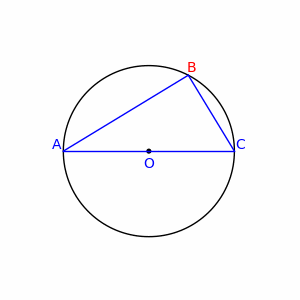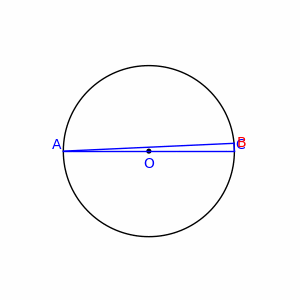
Source photo : Dino - Théorème des Milieux
La droite passant par les milieux de deux côtés d'un triangle est parallèle au 3ème côté de ce triangle.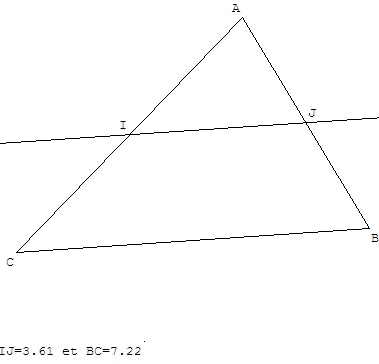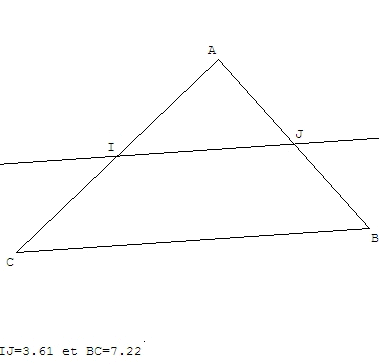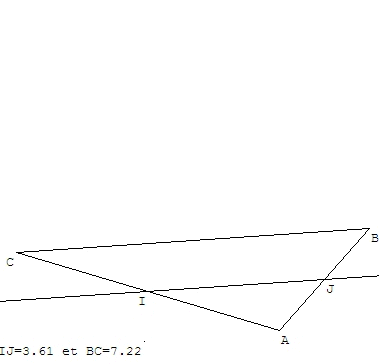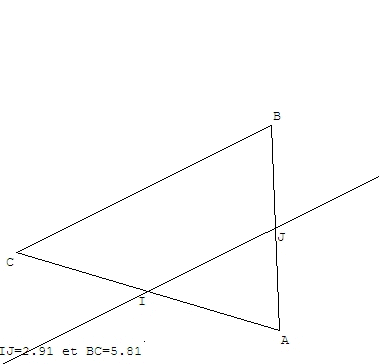
Source photo : Académie de Besançon - Pi
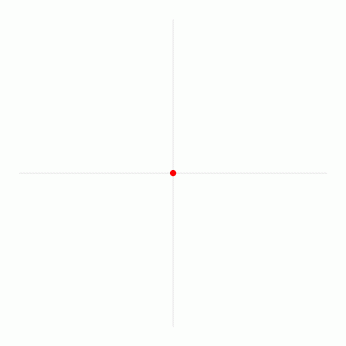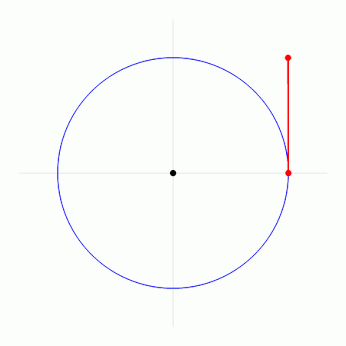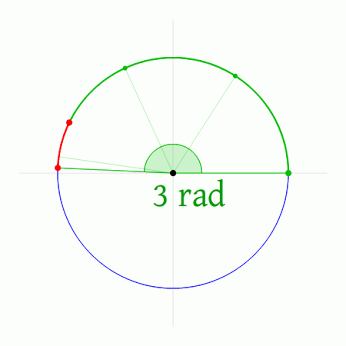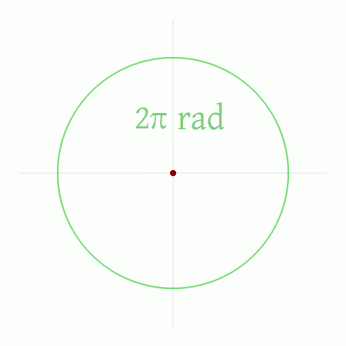
Le mystérieux nombre Pi est la circonférence du cercle de diamètre 1. Donc, pour calculer la circonférence d'un cercle, vous n'avez qu'à multiplier le diamètre par ce nombre.
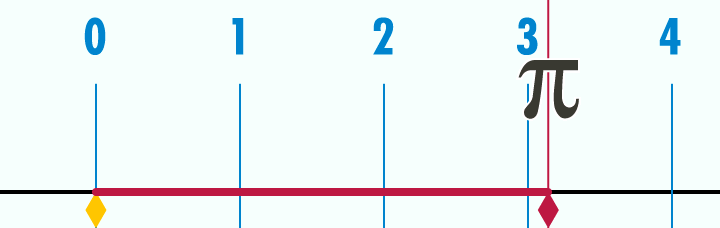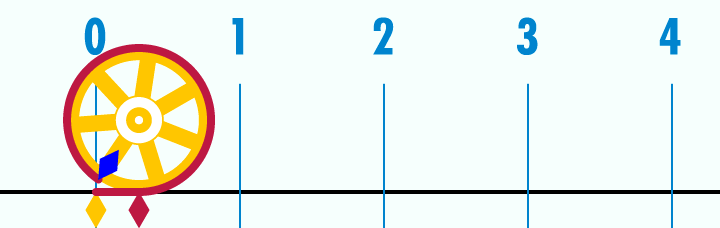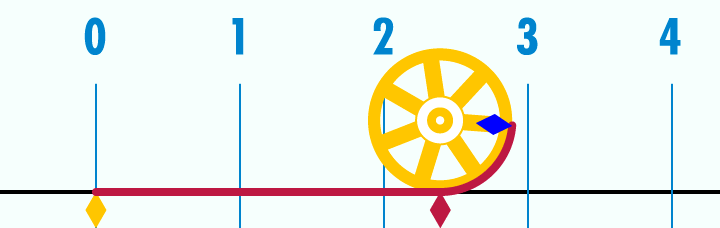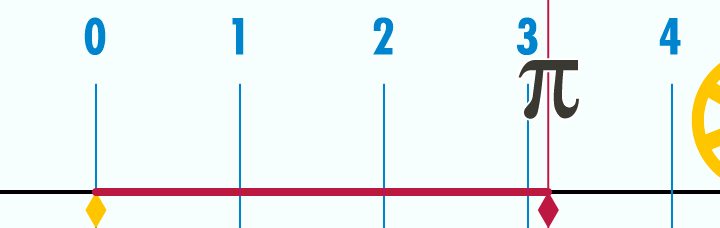
Sinon, on peut aussi l'expliquer comme ça :
- Les droites dramatiques
Elles se croisent une fois et s'oublient à jamais, elles se suivent sans jamais se rencontrer : mon Dieu que les maths peuvent être tristes.

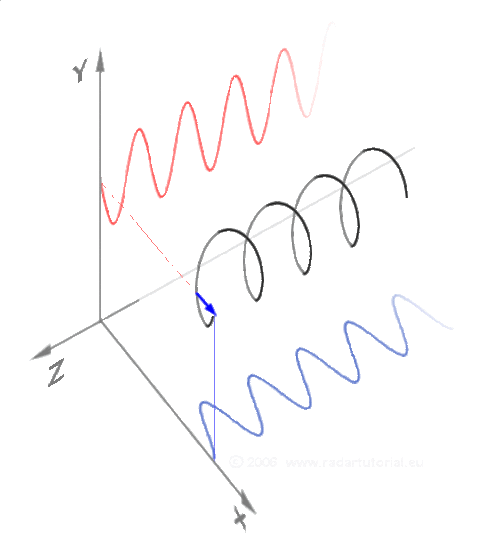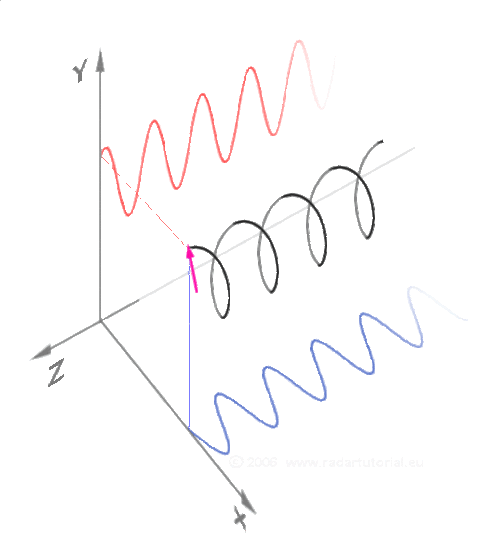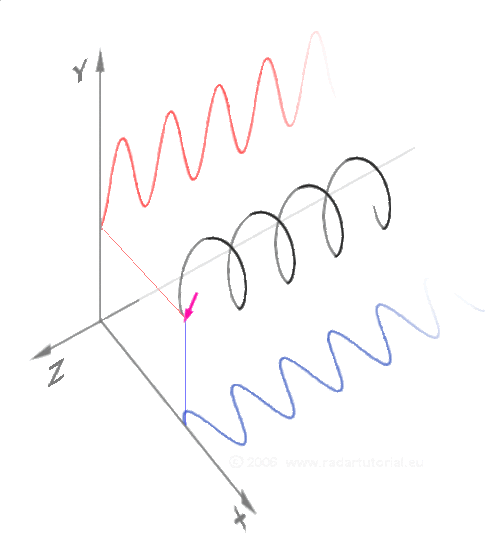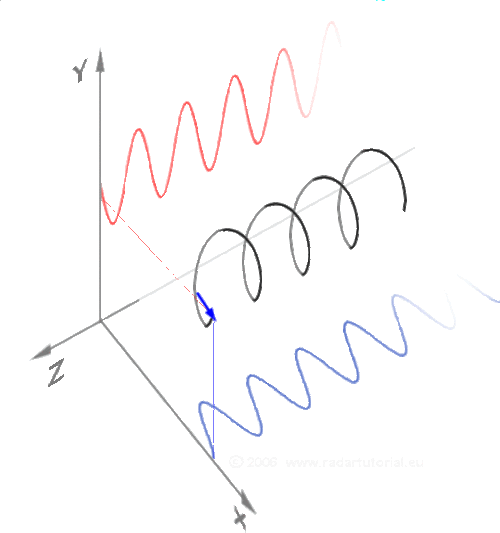
- Cosinus et sinus
Pas forcément simple de se représenter les fonctions trigonométriques. Vous faites le tour de l'horloge dans le plan, et à chaque fois que vous augmentez l'angle, l'évolution sur l'axe des X mesure le cosinus, celle sur l'axe des Y mesure le sinus.
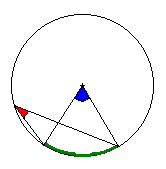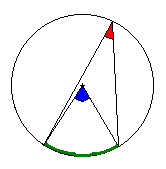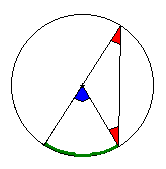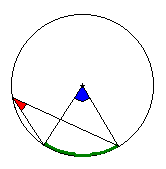
- Théorème de l'angle inscrit et de l'angle au centre
Dans un cercle, un angle au centre mesure le double d'un angle inscrit interceptant le même arc. Tracez un cercle, prenez deux points sur ce cercle, l'angle formé par le centre et ces deux points sera deux fois plus aigu que l'angle formé avec n'importe quel autre point du cercle. Dit comme ça, c'est compliqué. Avec un dessin qui bouge, c'est plus clair.
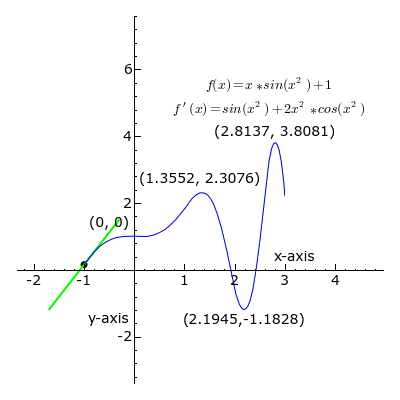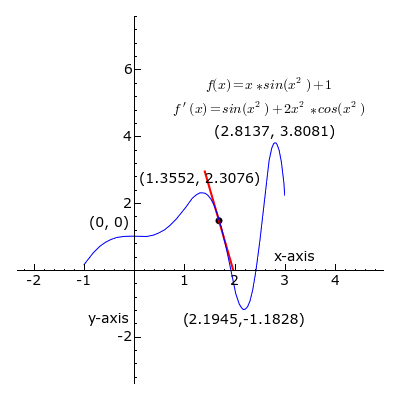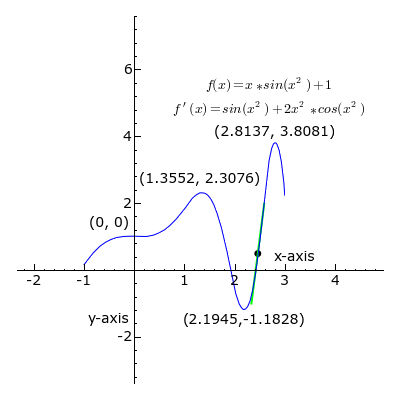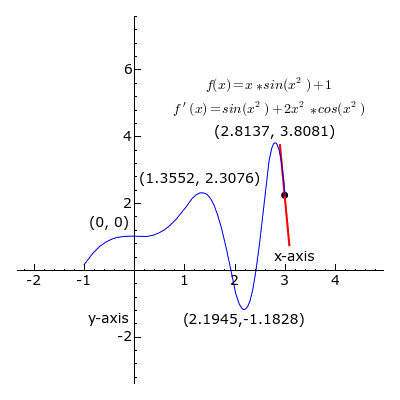
- Le calcul dérivé
Pour bien piger ce qu'est le nombre dérivé en un point d'une fonction, il suffit de le dessiner : la tangente est verte quand le coefficient directeur est positif, noir quand il est nul et rouge quand il est négatif. Si la courbe représente la vitesse au fil du temps, chacune de ces pentes représente l'accélération (ou la décélération).
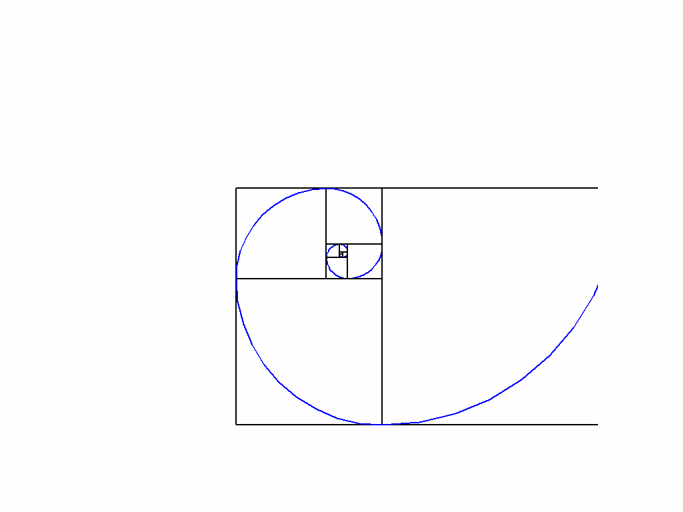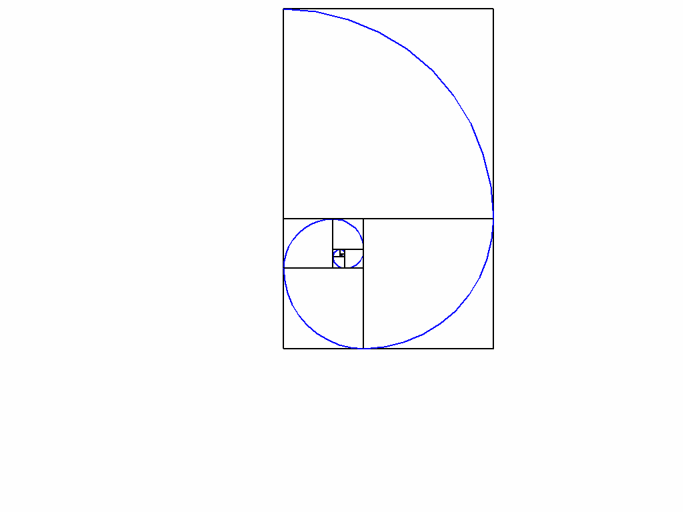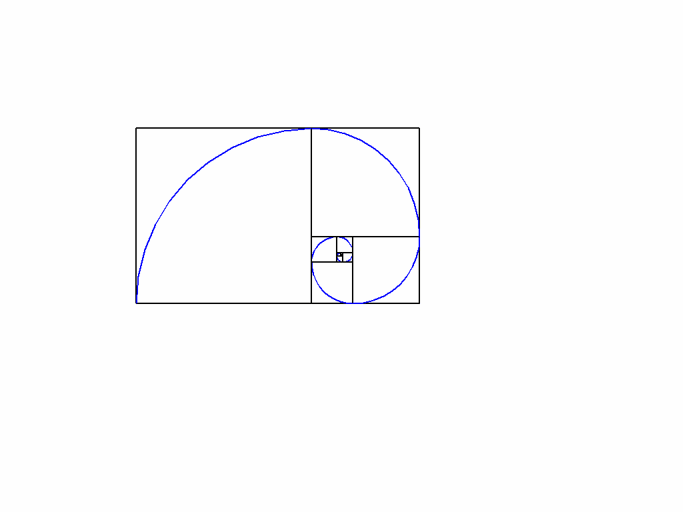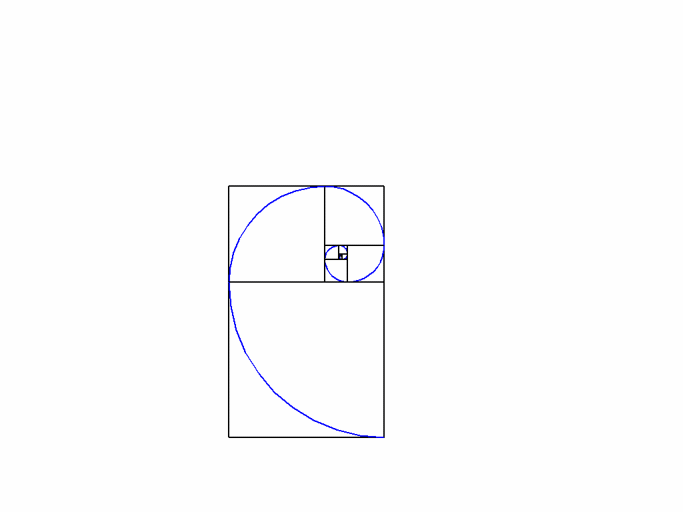
- Le Nombre d'Or
Ce rapport qui permet de faire des rectangle parfaitement harmonieux : ce rectangle a pour longueur a et pour largeur b et répond à l'égalité (a+b)/a = a/b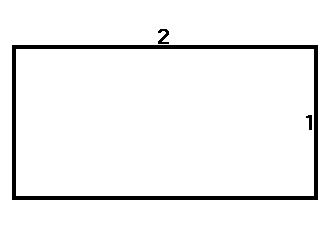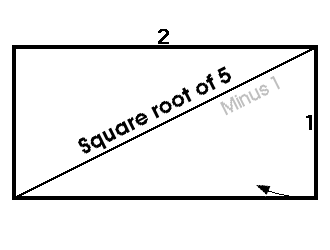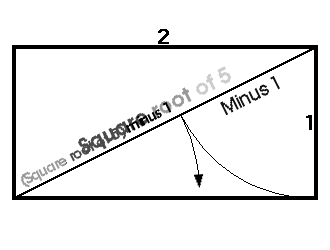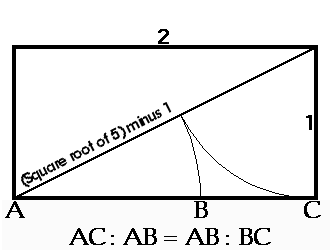
Une fois que vous avez ce rapport, construisez des "rectangles d'or" et des "spirales d'or' pour un monde plein d'harmonie :
- (bonus) Paradoxe du carré manquant
Si on découpe un triangle selon un quadrillage, de telle sorte que plusieurs reconstructions du triangle soient possibles, alors il y a certaines constructions où il manque un carré unitaire. Le résultat est en fait impossible et il s'agit d'une illusion d'optique.
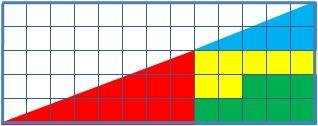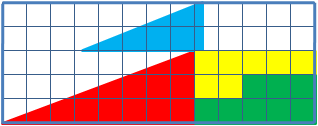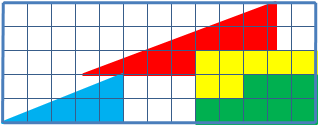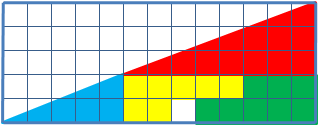
Le même avec du chocolat, pour bouffer gratos :

Ca y est, ça va mieux ?
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2025%2F03%2FVISITE-DISTILLERIE-CALVADOS.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2024%2F08%2FSITE-REVENTE-CONCERT-3.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2023%2F05%2Fmamouth2.jpeg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2024%2F04%2FWOMANIZER-ENHANCE.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2020%2F05%2FSommeil.png)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2025%2F03%2FPUZZLE-PHOTO-PERSONNALISER.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2025%2F03%2FINDISPENSABLES-ESCALADE.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2016%2F03%2Fstpatrick.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2023%2F07%2FMARQUE-PAGE-PERSONNALISE.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2023%2F03%2FConfinement.png)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2019%2F12%2Fphotos-noel-famille-genantes.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2023%2F12%2FTop-Tweets-Julien-Dore.png)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2020%2F11%2FKamoulox.png)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2019%2F07%2Fune_voisins.jpg)
:format(webp):quality(70)/https%3A%2F%2Fmedia.topito.com%2Fwp-content%2Fuploads%2F2020%2F06%2FFAUTE-FRANCAIS.jpg)